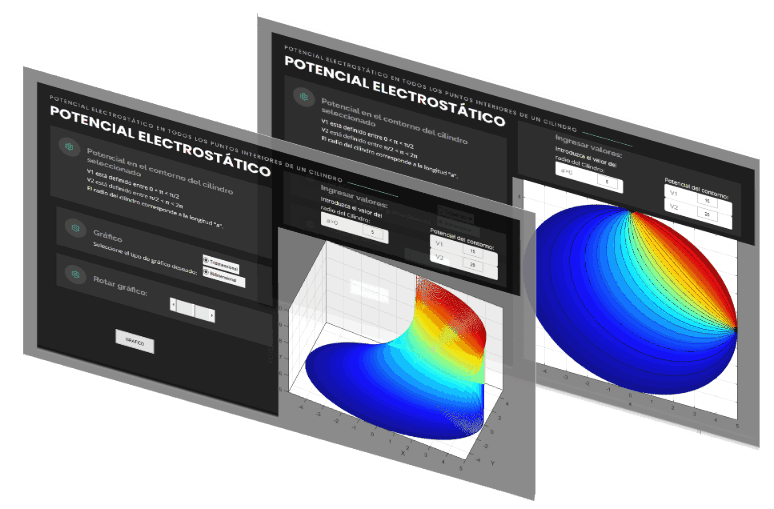
CALCULATOR OF POTENTIAL AND FIELD ELECTROSTATIC USING THE VARIABLE SEPARATION METHOD.
Case: hollow conductor cylinder.
By Gleysa Muñoz
Resume
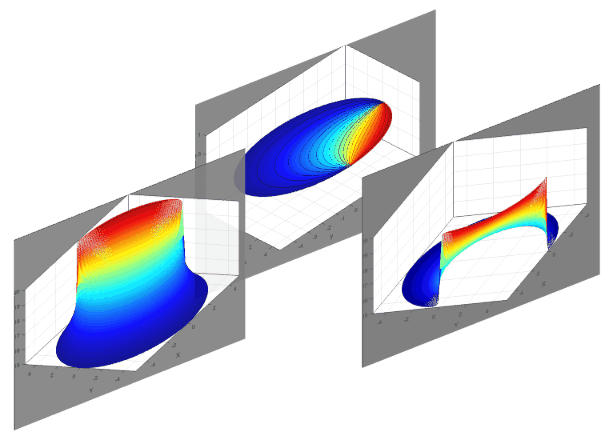
In this project the field and electrostatic potential of a hollow cylinder will be determined, sectioned into two parts and connected to different potentials, whose charge distribution is equal to zero. This project is developed in the GUIDE visual programming environment available in Matlab, with which it will graphically calculate the electrostatic power at all points inside the cylinder studied. The behavior of an electrostatic field is described through the Laplace and Poisson differential equations, which provide a potential expression for specific conditions of charge distribution. An electrostatic field does not vary with time and has an electrical effect at a distance. For this reason, the description of this effect does not depend on a temporal variable, but on the geometric conditions of the problem, the differences in applied potentials and the load distributions. When solving problems consisting of conductors that are found at a given potential and considering regions of space where the charge distributions are zero, an expression can be found that describes the behavior of the electrostatic field by solving Laplace's differential equation.


Goals
*Determine the mathematical expression of the potential and the field electrostatic inside a hollow conductive cylinder, free from charges and sectioned into two parts connected to different potentials through the solution of Laplace's equation by the method of separation of variables.
*Create a graphical user interface to calculate the value of the electrostatic potential in all the interior points of the conducting cylinder under study through the visual GUIDE programming environment available in Matlab.
*Calculate the value of the electrostatic potential at sixteen interior points of the conducting cylinder under study.
Potential calculator software
For applications that have to do with the study of electromagnetic fields, the need arises to use a computational tool that allows avoiding the difficulties of analytical studies, reducing the times in which answers to problems are obtained and allowing agile interpretation of the results.
These are important elements in application development at the engineering level. Therefore, it is necessary to use software capable of processing the Laplace equation that mathematically describes the electrostatic potential.